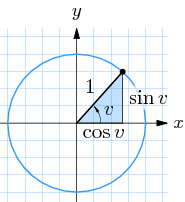Repetition Trigonometri

Innehållsförteckning

1.1 Rätvinkliga trianglar

Övningar

1.2 Godtyckliga trianglar

1.3 Trigon. identiteter  >>

Trigon = Triangel på latin. $\qquad\qquad\qquad\qquad\quad$ Trigonometri = Att mäta trianglar.

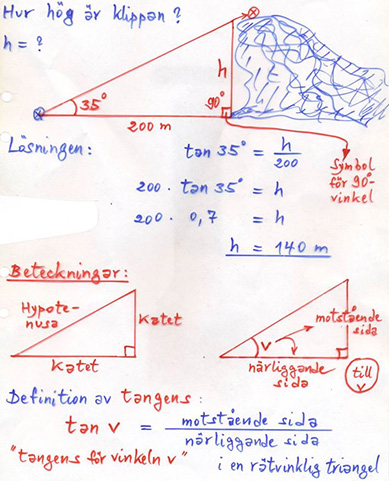
1.1 Trigonometri i rätvinkliga trianglar

Tangens för $\, v \, < \, 90^\circ$

Se även längre ned. Sinus och Cosinus för $\, v \, < \, 90^\circ$

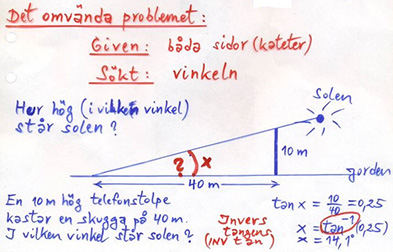
1.2 Trigonometri i godtyckliga trianglar

<<  Förra avsnitt: Genomgång rätvinkliga

Formelsamling Trigonometri

Nästa avsnitt  >>

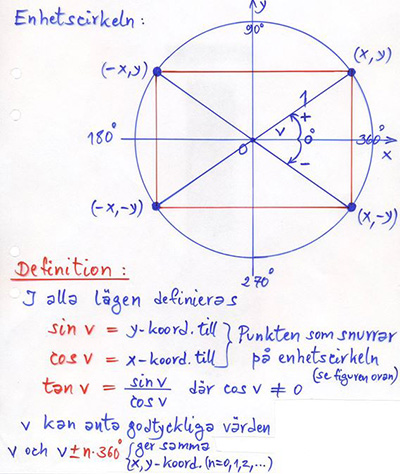
Enhetscirkeln

är cirkeln med radien $\, r \, = \, 1 \,$ och medelpunkten $\, M \, = \, O \,$ (origo).

Om en punkt $\, P\,(x, y) \,$ snurrar på enhetscirkeln och $\, v \,$ är vinkeln mellan $\, x$-axeln och $\, \overline{OP}$, så gäller:

$\qquad\qquad\quad$

$\begin{array}{rcl} x & = & \cos v \\ y & = & \sin v \end{array}$

I cirklar med radien $\, r \, > \, 1 \,$ förblir vinkeln $\, v \,$ den samma och därmed $\, \cos v = (r \cdot x) / r = x \,$ och $\, \sin v = (r \cdot y) / r = y$, precis som ovan.

Dvs formlerna för $\, x = \cos v \,$ och $\, y = \sin v \,$ stämmer fortfarande, även om $\, r \, > \, 1 \,$.

De här formlerna används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar $\, v \, \geq \, 90^\circ \,$.

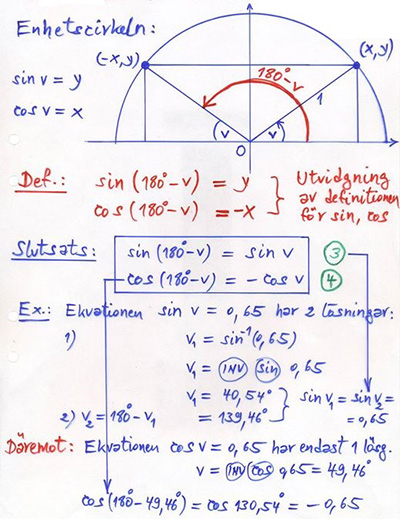
Sinus och Cosinus för vinklar i intervallet: $\quad 90^\circ \, \leq \, v \, \leq \, 180^\circ$

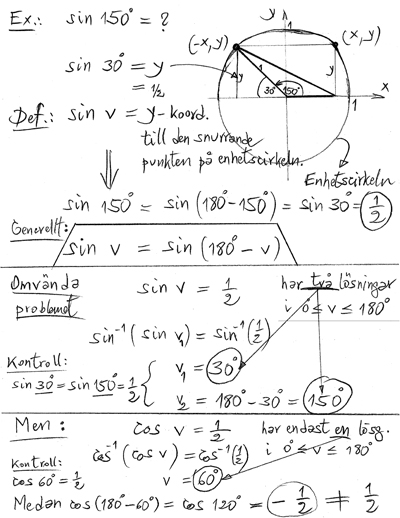
Exempel:

$$\sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, 1 / 2$$

$$\cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -(1 / 2)$$

Förklaring med enhetscirkeln:

Punkten till vinkeln $\, v \,$ har samma $\, y$-koordinat ($=\sin v$) som punkten till vinkeln $\, 180-v$.

Punkten till vinkeln $\, v \,$ har samma $\, x$-koordinat ($=\cos v$) som punkten till vinkeln $\, 180-v \,$ med omvänt tecken.

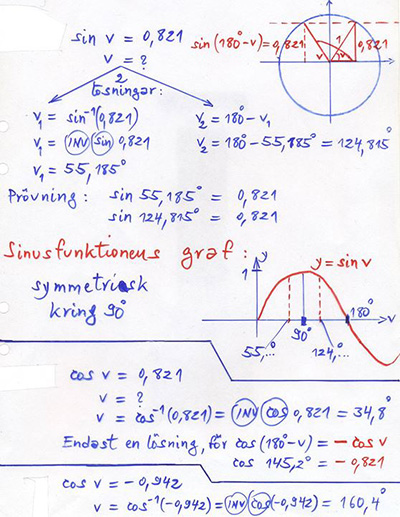
Ekvationer           med    Sin & Cos:

Sinus, Cosinus och Tangens för alla vinklar

En gång till      Sin & Cos   för $v \geq 90^\circ$    i trianglar:

Slutsatser

En sinusekvation har i intervallet $\, 0^\circ \leq v \leq 180^\circ \,$ alltid två lösningar.

En cosinusekvation har i intervallet $\, 0^\circ \leq v \leq 180^\circ \,$ endast en lösning.

Copyright © 2021 TechPages AB. All Rights Reserved.